后綴數(shù)組的一些基本概念請(qǐng)自行百度,簡(jiǎn)單來(lái)說(shuō)后綴數(shù)組就是一個(gè)字符串所有后綴大小排序后的一個(gè)集合,然后我們根據(jù)后綴數(shù)組的一些性質(zhì)就可以實(shí)現(xiàn)各種需求。
|
1
2
3
4
5
6
7
8
9
10
11
12
|
public class mysuffixarraytest { public char[] suffix;//原始字符串 public int n;//字符串長(zhǎng)度 public int[] rank;// suffix[i]在所有后綴中的排名 // (與rank是互逆運(yùn)算) public int[] height;// 表示suffix[sa[i]]和suffix[sa[i - 1]]的最長(zhǎng)公共前綴,也就是排名相鄰的兩個(gè)后綴的最長(zhǎng)公共前綴 public int[] h;// 等于height[rank[i]],也就是后綴suffix[i]和它前一名的后綴的最長(zhǎng)公共前綴 public int[] ws;// 計(jì)數(shù)排序輔助數(shù)組 public int[] y;// 第二關(guān)鍵字rank數(shù)組 public int[] x;// rank的輔助數(shù)組} |
以下的講解都以"aabaaaab"這個(gè)字符串為例,先展示一下結(jié)果,請(qǐng)參考這個(gè)結(jié)果進(jìn)行理解分析(這個(gè)結(jié)果圖我復(fù)制別人的,請(qǐng)各位默認(rèn)下標(biāo)減1,因?yàn)槲业臄?shù)組從下標(biāo)0開(kāi)始的)
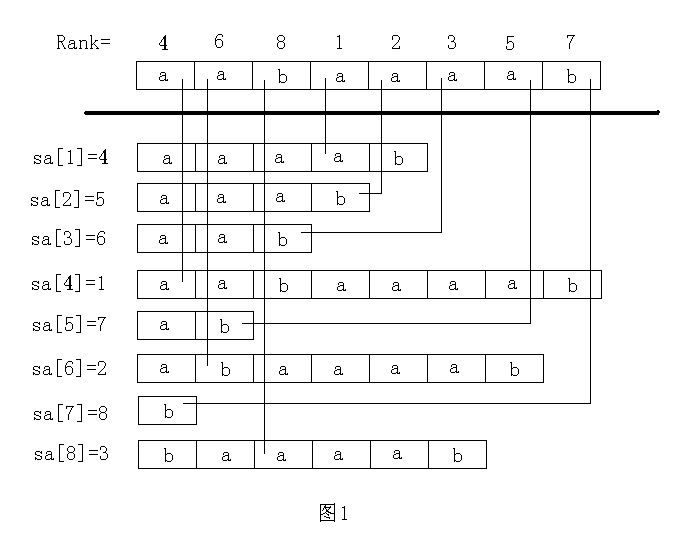
suffix:原始字符串?dāng)?shù)組 假設(shè)原始字符串是"aabaaaab" 那這個(gè)數(shù)組對(duì)應(yīng)的值應(yīng)該是{'a','a','b','a','a','a','a','b'}
n:字符串長(zhǎng)度 這里n是8
rank: 后綴數(shù)組的名次數(shù)組 相當(dāng)于存的是第i個(gè)后綴對(duì)應(yīng)的名次是多少 比如rank[0]就是指"aabaaaab"這個(gè)后綴的名次 rank[1]指"abaaaab"這個(gè)后綴的名次
sa: 這個(gè)是和rank數(shù)組互逆的一個(gè)數(shù)組 存的是第x名的是哪個(gè)后綴 還是舉例子來(lái)說(shuō)明 sa[0]指的是排名第一的后綴數(shù)組即為3 也就是"aaaab"這個(gè)數(shù)組 他對(duì)應(yīng)的rank[3]就是0。 sa[rank[i]]=i 這個(gè)式子請(qǐng)務(wù)必理解,理解了這個(gè)sa和rank的關(guān)系你應(yīng)該也搞懂了
height: height[i]就是sa[i]后綴數(shù)組和sa[i-1]后綴數(shù)組的最大公共前綴的長(zhǎng)度 height[1]指的是排名第2和排名第1的最大公共前綴 sa[1]與sa[0]即"aaab"與"aaaab"的最大公共前綴 自然一眼看出 height[1]=3
h: h[i]指的是第i個(gè)后綴與他前一名的最大公共前綴 h[0]指的就是第一個(gè)后綴數(shù)組即"aabaaaab"與他前一名即"aab"的最大公共前綴 也就是height[rank[0]]=height[3]=3 這個(gè)有點(diǎn)不好理解 可以暫時(shí)不理解 繼續(xù)往下看
ws: 沒(méi)什么好說(shuō)的,計(jì)數(shù)排序的輔助數(shù)組
y: 存的是第二關(guān)鍵字排序 相當(dāng)于第二關(guān)鍵字的sa數(shù)組
x: 你可以理解為rank數(shù)組的備份,他最開(kāi)始是rank數(shù)組備份,之后記錄每次循環(huán)后的rank數(shù)組
首先來(lái)看下求sa數(shù)組的代碼,我會(huì)一段一段的說(shuō)明代碼作用并在后面附上總代碼
|
1
2
3
4
5
6
7
8
9
|
rank = new int[n]; sa = new int[n]; ws = new int[255]; y = new int[n]; x = new int[n]; // 循環(huán)原字符串轉(zhuǎn)換int值放入rank數(shù)組 for (int i = 0; i < n; i++) { rank[i] = (int) suffix[i]; } |
上面這段代碼的作用就是初始化數(shù)組以及進(jìn)行第一次計(jì)數(shù)排序,第一次循環(huán)是對(duì)rank數(shù)組賦初值,執(zhí)行完后rank數(shù)組對(duì)應(yīng)值為{97,97,98,97,97,97,97,98},大家應(yīng)該看得出來(lái)rank數(shù)組的初值就是字母對(duì)應(yīng)的ascii碼。
接下來(lái)的三段循環(huán)就是第一次計(jì)數(shù)排序了,不理解計(jì)數(shù)排序的請(qǐng)百度。我說(shuō)下這三段循環(huán)運(yùn)行的過(guò)程
|
1
2
3
4
5
6
7
|
for (int i = 0; i < n; i++) { ws[rank[i]]++; x[i] = rank[i]; }for (int i = 1; i < ws.length; i++) { ws[i] += ws[i - 1]; } |
這兩段循環(huán)做的是對(duì)所有出現(xiàn)值計(jì)數(shù),并備份rank數(shù)組至x數(shù)組,第一個(gè)循環(huán)運(yùn)行完后ws[97]=6,ws[98]=2,第二個(gè)循環(huán)運(yùn)行完后ws[97]=6,ws[98]=8
|
1
2
3
|
for (int i = n - 1; i >= 0; i--) { sa[--ws[rank[i]]] = i; } |
上面這段就是具體的計(jì)數(shù)排序求sa數(shù)組的代碼,大家第一次看的時(shí)候肯定是蒙的,這怎么就求出了sa呢。我第一次也是蒙的,但請(qǐng)保持耐心,仔細(xì)理解這段代碼。還記得前面說(shuō)的公式嗎 sa[rank[i]]=i 舉個(gè)例子對(duì)于后綴"b"我們求他的sa 即sa[rank[7]]=sa[98]=7 顯然sa[98]不存在 但我們將98出現(xiàn)的次數(shù)已經(jīng)記錄在ws數(shù)組了 那么ws[98]應(yīng)該就是"b"對(duì)應(yīng)的名次了 注意不要忘記計(jì)數(shù)減1 就變成了 sa[--ws[rank[i]]] = i。至于為什么要從后向前遍歷,這里你需要仔細(xì)理解一下,否則后面根據(jù)第二關(guān)鍵字進(jìn)行排序的方式你肯定會(huì)完全蒙蔽。如果有兩個(gè)rank值相同的你怎么排序呢?肯定是先出現(xiàn)的在sa數(shù)組的前面,仔細(xì)思考這個(gè)循環(huán)以及ws數(shù)組值的變化,你會(huì)明白,for循環(huán)的順序?qū)嶋H上代表了rank值相同時(shí)的排列順序。從后向前遍歷代表了rank值相同時(shí)靠后的后綴排名也靠后。
以上只是第一次計(jì)數(shù)排序,相當(dāng)于只比較每個(gè)后綴數(shù)組的首字母求出了一個(gè)sa,對(duì)應(yīng)的結(jié)果如下圖

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
// 循環(huán)組合排序 for (int j = 1, p = 0; j <= n; j = j << 1) { // 需要補(bǔ)位的先加入排序數(shù)組y p = 0; for (int i = n - j; i < n; i++) { y[p++] = i; } // 根據(jù)第一關(guān)鍵字sa排出第二關(guān)鍵字 for (int i = 0; i < n; i++) { if (sa[i] >= j) { y[p++] = sa[i] - j; } } // 合并兩個(gè)關(guān)鍵字的排序 for (int i = 0; i < ws.length; i++) { ws[i] = 0; } for (int i : x) { ws[i]++; } for (int i = 1; i < ws.length; i++) { ws[i] += ws[i - 1]; } for (int i = n - 1; i >= 0; i--) { sa[--ws[x[y[i]]]] = y[i]; y[i] = 0; } // 根據(jù)sa算出rank數(shù)組 int xb[] = new int[n];// x數(shù)組備份 for (int i = 0; i < n; i++) { xb[i] = x[i]; } int number = 1; x[sa[0]] = 1; for (int i = 1; i < n; i++) { if (xb[sa[i]] != xb[sa[i - 1]]) { x[sa[i]] = ++number; } else if (sa[i] + j >= n && sa[i - 1] + j >= n) { x[sa[i]] = number; } else if (sa[i] + j < n && sa[i - 1] + j >= n) { x[sa[i]] = ++number; } else if (xb[sa[i] + j] != xb[sa[i - 1] + j]) { x[sa[i]] = ++number; } else { x[sa[i]] = number; } if (number >= n) break; } } |
這是求sa數(shù)組最難以理解的一段代碼,首先大家需要理解一下倍增算法的思路。第一次計(jì)數(shù)排序后我們是不是已經(jīng)知道了所有后綴數(shù)組第一個(gè)首字母的排序,既然我們知道了第一個(gè)首字母的排序那是不是相當(dāng)于我們也知道了他第二個(gè)字母的順序(注意排序和順序的區(qū)別,排序是我們知道他固定的排在第幾名,順序是我們只知道他出現(xiàn)的次序,但并不知道他具體排第幾名),這是當(dāng)然的,因?yàn)樗麄儽緛?lái)就是出自一個(gè)字符串,對(duì)于每個(gè)后綴他同時(shí)也可以作為他之前后綴的后綴。說(shuō)起來(lái)繞口,舉個(gè)例子,比如對(duì)于"baaaab"他首字母的順序是不是對(duì)應(yīng)"abaaaab"的第二關(guān)鍵字順序。我們有了第一關(guān)鍵字的排序和第二關(guān)鍵字的排序就能求出兩個(gè)關(guān)鍵字的組合排序,跟據(jù)組合排序的結(jié)果我們還是可以延用之前的想法,對(duì)于"baaaab"第一次組合排序后我們排出來(lái)他頭兩個(gè)字母"ba"的排序,那么他同時(shí)他也可以作為"aabaaaab"的第二關(guān)鍵字的順序。整個(gè)排序的邏輯參考下圖

然后我們來(lái)分段的分析代碼
|
1
2
3
4
5
6
7
8
9
|
for (int i = n - j; i < n; i++) { y[p++] = i; } // 根據(jù)第一關(guān)鍵字sa排出第二關(guān)鍵字for (int i = 0; i < n; i++) { if (sa[i] >= j) { y[p++] = sa[i] - j; } } |
以上代碼就是求第二關(guān)鍵字的sa也就是y數(shù)組,p初始值為0,第一段循環(huán)是將需要補(bǔ)位的后綴排在數(shù)組最前面。
第二個(gè)循環(huán)的邏輯你需要結(jié)合前面的邏輯圖進(jìn)行理解了,我們對(duì)第一關(guān)鍵字的排序結(jié)果sa進(jìn)行遍歷,if(sa[i] >=j )判斷該后綴能否作為其他后綴的第二關(guān)鍵字,以第一次循環(huán)j=1為例,當(dāng)sa[i]=0時(shí)代表后綴數(shù)組"aabaaaab",顯然它無(wú)法作為其他后綴的第二關(guān)鍵字。對(duì)于可以作為其他后綴第二關(guān)鍵字的,他sa的順序就是對(duì)應(yīng)的第二關(guān)鍵字的順序,sa[i] - j 求出他作為第二關(guān)鍵字的后綴放在y數(shù)組下,并且p++。這里你需要慢慢理解。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
// 合并兩個(gè)關(guān)鍵字的排序 for (int i = 0; i < ws.length; i++) { ws[i] = 0; } for (int i : x) { ws[i]++; } for (int i = 1; i < ws.length; i++) { ws[i] += ws[i - 1]; } for (int i = n - 1; i >= 0; i--) { sa[--ws[x[y[i]]]] = y[i]; y[i] = 0; } |
以上是根據(jù)第一關(guān)鍵字排序sa和第二關(guān)鍵字排序y求出其組合排序,這段代碼相當(dāng)?shù)幕逎y懂。我們可以先不理解代碼,先理解一個(gè)思路,對(duì)于兩個(gè)關(guān)鍵字排序,實(shí)際規(guī)則和兩個(gè)數(shù)字排序差不多,比如11和12比較大小,10位就是第一關(guān)鍵字,個(gè)位就是第二關(guān)鍵字,比較完10位我們求得11=12,再比較個(gè)位我們知道11<12,10位相同的話(huà)其個(gè)位的順序就是大小順序。我上面第一次計(jì)數(shù)排序時(shí)說(shuō)過(guò),計(jì)數(shù)排序for循環(huán)的順序?qū)嶋H上代表了rank值相同時(shí)的排列順序,那么這里我們?cè)趺匆淮斡?jì)數(shù)排序就求出兩個(gè)關(guān)鍵字合并后的順序呢?我說(shuō)下我的理解,一次計(jì)數(shù)排序?qū)嶋H上包含了兩次排序,一次是數(shù)值的排序,一次是出現(xiàn)次序的排序,其規(guī)則就相當(dāng)于前面11和12比較的例子,數(shù)值的排序是10位,出現(xiàn)次序的排序是個(gè)位。到這里我們就有思路了,數(shù)值的排序用第一關(guān)鍵字的排序,出現(xiàn)次序的排序用第二關(guān)鍵字的排序,這樣就能一次計(jì)數(shù)排序求得兩個(gè)關(guān)鍵字合并后的排序。上面的代碼就是這個(gè)思路的實(shí)現(xiàn)。x數(shù)組就是第一關(guān)鍵字的rank數(shù)組,我們對(duì)他進(jìn)行計(jì)數(shù)。
|
1
2
3
4
|
for (int i = n - 1; i >= 0; i--) { sa[--ws[x[y[i]]]] = y[i]; y[i] = 0; } |
這段循環(huán)就是上面所有思路的實(shí)現(xiàn),我們對(duì)第二關(guān)鍵字?jǐn)?shù)組y從后進(jìn)行遍歷,對(duì)于y[i]我們求出他第一關(guān)鍵字的計(jì)數(shù)排名,這個(gè)計(jì)數(shù)排名就是y[i]的排名,最后計(jì)數(shù)減1。合并關(guān)鍵字的排序成功求出。
相信你如果理解了上面所有的代碼后肯定會(huì)拍案叫絕,我本人在一遍遍琢磨這段代碼時(shí)也是熱血澎湃,簡(jiǎn)直拜服了。這就是算法的魅力吧。
有了sa數(shù)組我們就可以求rank數(shù)組,這并不難,也就不講解了。下面附上求sa的所有代碼。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
|
public static void main(string[] args) { string str = "aabaaaab"; mysuffixarraytest arraytest = new mysuffixarraytest(str.tostring()); arraytest.initsa();// 求sa數(shù)組 } public void initsa() { rank = new int[n]; sa = new int[n]; ws = new int[255]; y = new int[n]; x = new int[n]; // 循環(huán)原字符串轉(zhuǎn)換int值放入rank數(shù)組 for (int i = 0; i < n; i++) { rank[i] = (int) suffix[i]; } // 第一次計(jì)數(shù)排序 for (int i = 0; i < n; i++) { ws[rank[i]]++; x[i] = rank[i]; } for (int i = 1; i < ws.length; i++) { ws[i] += ws[i - 1]; } for (int i = n - 1; i >= 0; i--) { sa[--ws[rank[i]]] = i; } // 循環(huán)組合排序 for (int j = 1, p = 0; j <= n; j = j << 1) { // 需要補(bǔ)位的先加入排序數(shù)組y p = 0; for (int i = n - j; i < n; i++) { y[p++] = i; } // 根據(jù)第一關(guān)鍵字sa排出第二關(guān)鍵字 for (int i = 0; i < n; i++) { if (sa[i] >= j) { y[p++] = sa[i] - j; } } // 合并兩個(gè)關(guān)鍵字的排序 for (int i = 0; i < ws.length; i++) { ws[i] = 0; } for (int i : x) { ws[i]++; } for (int i = 1; i < ws.length; i++) { ws[i] += ws[i - 1]; } for (int i = n - 1; i >= 0; i--) { sa[--ws[x[y[i]]]] = y[i]; y[i] = 0; } // 根據(jù)sa算出rank數(shù)組 int xb[] = new int[n];// x數(shù)組備份 for (int i = 0; i < n; i++) { xb[i] = x[i]; } int number = 1; x[sa[0]] = 1; for (int i = 1; i < n; i++) { if (xb[sa[i]] != xb[sa[i - 1]]) { x[sa[i]] = ++number; } else if (sa[i] + j >= n && sa[i - 1] + j >= n) { x[sa[i]] = number; } else if (sa[i] + j < n && sa[i - 1] + j >= n) { x[sa[i]] = ++number; } else if (xb[sa[i] + j] != xb[sa[i - 1] + j]) { x[sa[i]] = ++number; } else { x[sa[i]] = number; } if (number >= n) break; } } } |
總結(jié)
以上所述是小編給大家介紹的java后綴數(shù)組之求sa數(shù)組的實(shí)例代碼,希望對(duì)大家有所幫助,如果大家有任何疑問(wèn)請(qǐng)給我留言,小編會(huì)及時(shí)回復(fù)大家的。在此也非常感謝大家對(duì)服務(wù)器之家網(wǎng)站的支持!
原文鏈接:https://www.cnblogs.com/mengzhang/p/8919870.html