漢諾塔
法國數學家愛德華?盧卡斯曾編寫過一個印度的古老傳說:在世界中心貝拿勒斯(在印度北部)的圣廟里,一塊黃銅板上插著三根寶石針。印度教的主神梵天在創造世界的時候,在其中一根針上從下到上地穿好了由大到小的64片金片,這就是所謂的漢諾塔。不論白天黑夜,總有一個僧侶在按照下面的法則移動這些金片:一次只移動一片,不管在哪根針上,小片必須在大片上面。僧侶們預言,當所有的金片都從梵天穿好的那根針上移到另外一根針上時,世界就將在一聲霹靂中消滅,而梵塔、廟宇和眾生也都將同歸于盡。
這個傳說挺有意思的,這個傳說是說有64片金片。但我們要討論是只有3片或4片金片。看看網圖吧。


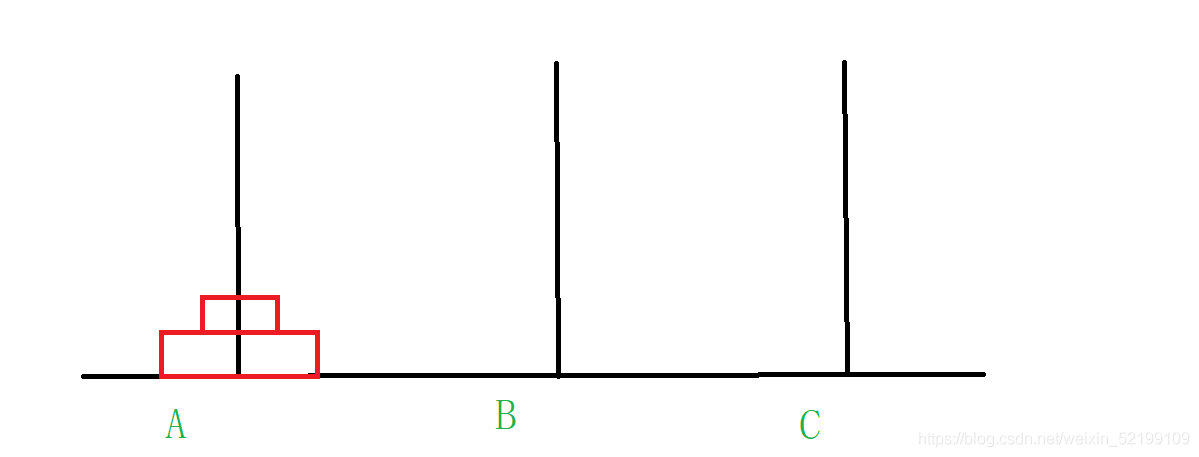
我們以三片開始討論。而討論題目開始先明白,這個柱子的位置并不影響移動,只是特定的柱子才是關鍵。
我們來看看如果只有一個金片,要移動多少次。

很明顯,只要一次就夠了。
再來看看兩片金片。
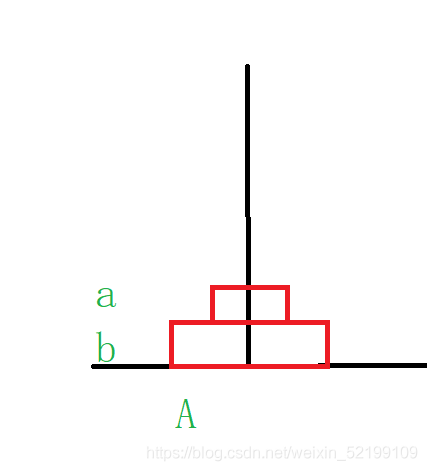
由于要全移動到C柱
1:
a:A->B
2:
b:A->C
3;
a:B->C
三步就可以全移動過去。
或者想要移動b片要先移動a片,將空C柱留給b片,去考慮a片的移動。
再來看看三片的移動

再來根據上面的思路,要想移動c片,得先移動a和b兩片,把C柱留給c片。
要先滿足這個條件

且大不能在小上面。要先移成這個樣子。

且,要滿足這個樣子得,先這樣。

總結一下
第一步

第二步

第三步

這么看下來,跟先前我們探討只移兩片,就沒什么區別了。
再將c片移動到C柱。

成了這個樣子。再來看看,我文章開頭說的,柱子的位置不是關鍵,位置是可以改變,只是要移動到特定的柱子。現在這樣,像不像,我們先前去移動兩個金片的步驟?
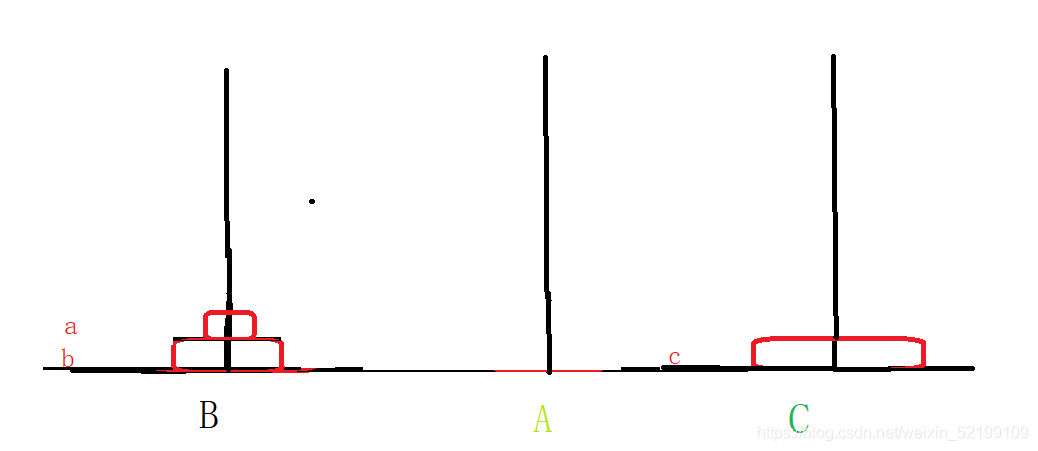
看清楚,這個樣子,就是移動兩個金片的步驟。再按上面的方法步驟,就行了。
我們來計算一下這寫步驟
第一部分:
移動兩個金片到B柱。
第二部分:
移動C片到C柱
第三部分:
在移動兩個金片到C柱。
總結一下
就是移兩個金片的步驟,移兩次,再移一次最下面的金片。總共2*3+1==7次。
再來看看四個金片的步驟。
要想移動這四個金片,必需要將這最下面的金片移動

這樣來看,分兩部分。
一:
移動d片到C柱
二:
移動a.b.c這仨個金片到C柱。
與上面移三片類比,、
第 一目的
第 二目的

第三目的

可以分三部完成。可見三片移法要移兩次。
就是2*7+1==15次。
依此類推
當移動N片金片時,要先考慮,
一C>移動這N-1片金片。
二C>再移第N片,
三C>再移動那N-1片到目的地。
可以分這三步。
柱子的位置對移動并沒有上面影響。
看代碼,這是計算次數的代碼。
#include <stdio.h>
int hanoi(int n)
{
if (n >= 2)
return 2 * hanoi(n - 1) + 1;
return 1;
}
int main(void)
{
printf("Problem of Hanoi\n");
printf("please input the number for problem:>\n");
int n;
scanf("%d", &n);
printf("%d",hanoi(n));
return 0;
}
這是編譯步驟的代碼
#include <stdio.h>
void move(char start,char end,int n)
{
static int count = 0;
count++;
printf("NO.%d step,the %d moves from %c to %c\n", count, n, start, end);
}
void hanoi(int n,char pose1,char pose2,char pose3)
{
if (n == 1)
move(pose1, pose3, 1);//一個是特例,不存在中間位置
else
{
hanoi(n - 1, pose1, pose3, pose2);//對應第一次移動N-1個金片
move(pose1, pose3, n);//對應移動第N個金片
hanoi(n - 1, pose2, pose1, pose3);//最后一次移動N-1個金片
}
}
int main(void)
{
char pose1 = 'A';//起始位置
char pose2 = 'B';//中間位置
char pose3 = 'C';//結束位置
int n;
scanf("%d", &n);
hanoi(n, pose1, pose2, pose3);
return 0;
}
使用遞歸時,要將其理解成一個功能模塊,而不是一步一步去分析。使用它的功能,同時確定終止條件并接近這個條件。
運用遞歸寫函數,可以”輕松“計算。
只為加深自己理解,含有學生氣,勿笑。
如有問題,煩請指點一二。
以上就是C語言編程遞歸算法實現漢諾塔的詳細內容,更多關于C語言遞歸算法的資料請關注服務器之家其它相關文章!
原文鏈接:https://blog.csdn.net/weixin_52199109/article/details/113003580