平面區(qū)域填充算法是計(jì)算機(jī)圖形學(xué)領(lǐng)域的一個(gè)很重要的算法，區(qū)域填充即給出一個(gè)區(qū)域的邊界（也可以是沒(méi)有邊界，只是給出指定顏色），要求將邊界范圍內(nèi)的所有象素單元都修改成指定的顏色（也可能是圖案填充）。區(qū)域填充中最常用的是多邊形填色，本文中我們就討論幾種多邊形區(qū)域填充算法。

一、種子填充算法（Seed Filling）

如果要填充的區(qū)域是以圖像元數(shù)據(jù)方式給出的，通常使用種子填充算法（Seed Filling）進(jìn)行區(qū)域填充。種子填充算法需要給出圖像數(shù)據(jù)的區(qū)域，以及區(qū)域內(nèi)的一個(gè)點(diǎn)，這種算法比較適合人機(jī)交互方式進(jìn)行的圖像填充操作，不適合計(jì)算機(jī)自動(dòng)處理和判斷填色。根據(jù)對(duì)圖像區(qū)域邊界定義方式以及對(duì)點(diǎn)的顏色修改方式，種子填充又可細(xì)分為幾類，比如注入填充算法（Flood Fill Algorithm）、邊界填充算法（Boundary Fill Algorithm）以及為減少遞歸和壓棧次數(shù)而改進(jìn)的掃描線種子填充算法等等。

所有種子填充算法的核心其實(shí)就是一個(gè)遞歸算法，都是從指定的種子點(diǎn)開(kāi)始，向各個(gè)方向上搜索，逐個(gè)像素進(jìn)行處理，直到遇到邊界，各種種子填充算法只是在處理顏色和邊界的方式上有所不同。在開(kāi)始介紹種子填充算法之前，首先也介紹兩個(gè)概念，就是“4-聯(lián)通算法”和“8-聯(lián)通算法”。既然是搜索就涉及到搜索的方向問(wèn)題，從區(qū)域內(nèi)任意一點(diǎn)出發(fā)，如果只是通過(guò)上、下、左、右四個(gè)方向搜索到達(dá)區(qū)域內(nèi)的任意像素，則用這種方法填充的區(qū)域就稱為四連通域，這種填充方法就稱為“4-聯(lián)通算法”。如果從區(qū)域內(nèi)任意一點(diǎn)出發(fā)，通過(guò)上、下、左、右、左上、左下、右上和右下全部八個(gè)方向到達(dá)區(qū)域內(nèi)的任意像素，則這種方法填充的區(qū)域就稱為八連通域，這種填充方法就稱為“8-聯(lián)通算法”。如圖1（a）所示，假設(shè)中心的藍(lán)色點(diǎn)是當(dāng)前處理的點(diǎn)，如果是“4-聯(lián)通算法”，則只搜索處理周圍藍(lán)色標(biāo)識(shí)的四個(gè)點(diǎn)，如果是“8-聯(lián)通算法”則除了處理上、下、左、右四個(gè)藍(lán)色標(biāo)識(shí)的點(diǎn)，還搜索處理四個(gè)紅色標(biāo)識(shí)的點(diǎn)。兩種搜索算法的填充效果分別如如圖1（b）和圖1（c）所示，假如都是從黃色點(diǎn)開(kāi)始填充，則“4-聯(lián)通算法”如圖1（b）所示只搜索填充左下角的區(qū)域，而“8-聯(lián)通算法”則如圖1（c）所示，將左下角和右上角的區(qū)域都填充了。

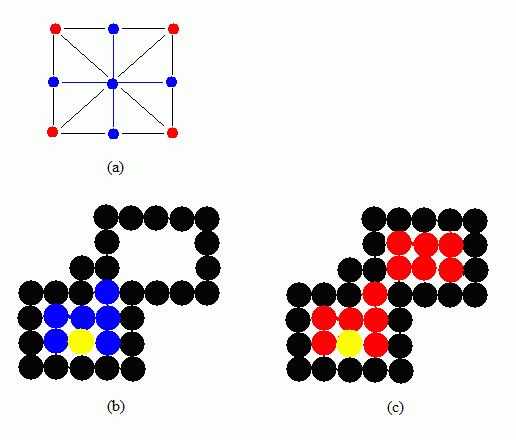
圖（1） “4-聯(lián)通”和“8-聯(lián)通”填充效果

并不能僅僅因?yàn)閳D1的填充效果就認(rèn)為“8-聯(lián)通算法”一定比“4-聯(lián)通算法”好，應(yīng)該根據(jù)應(yīng)用環(huán)境和實(shí)際的需求選擇聯(lián)通搜索方式，在很多情況下，只有“4-聯(lián)通算法”才能得到正確的結(jié)果。

1.1 注入填充算法（Flood Fill Algorithm）

 注入填充算法不特別強(qiáng)調(diào)區(qū)域的邊界，它只是從指定位置開(kāi)始，將所有聯(lián)通區(qū)域內(nèi)某種指定顏色的點(diǎn)都替換成另一種顏色，從而實(shí)現(xiàn)填充效果。注入填充算法能夠?qū)崿F(xiàn)顏色替換之類的功能，這在圖像處理軟件中都得到了廣泛的應(yīng)用。注入填充算法的實(shí)現(xiàn)非常簡(jiǎn)單，核心就是遞歸和搜索，以下就是注入填充算法的一個(gè)實(shí)現(xiàn)：

 for循環(huán)實(shí)現(xiàn)了向8個(gè)聯(lián)通方向的遞歸搜索，秘密就在direction_8的定義：

DIRECTION direction_8[] = { {-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {-1, -1} };

這個(gè)是搜索類算法中常用的技巧，無(wú)需做太多說(shuō)明，其實(shí)只要將其替換成如下direction_4的定義，就可以將算法改成4個(gè)聯(lián)通方向填充算法：

80 DIRECTION direction_4[] = { {-1, 0}, {0, 1}, {1, 0}, {0, -1} };

圖2就是應(yīng)用本算法實(shí)現(xiàn)的“4-聯(lián)通”和“8-聯(lián)通”填充效果：

圖（2） 注入填充算法實(shí)現(xiàn)

1.2 邊界填充算法（Boundary Fill Algorithm）

 邊界填充算法與注入填充算法的本質(zhì)其實(shí)是一樣的，都是遞歸和搜索，區(qū)別只在于對(duì)邊界的確認(rèn)，也就是遞歸的結(jié)束條件不一樣。注入填充算法沒(méi)有邊界的概念，只是對(duì)聯(lián)通區(qū)域內(nèi)指定的顏色進(jìn)行替換，而邊界填充算法恰恰強(qiáng)調(diào)邊界的存在，只要是邊界內(nèi)的點(diǎn)無(wú)論是什么顏色，都替換成指定的顏色。邊界填充算法在應(yīng)用上也非常的廣泛，畫(huà)圖軟件中的“油漆桶”功能就是邊界填充算法的例子。以下就是邊界填充算法的一個(gè)實(shí)現(xiàn)：

關(guān)于direction_8的說(shuō)明請(qǐng)參考上一節(jié)，圖3就是應(yīng)用本算法實(shí)現(xiàn)的“4-聯(lián)通”和“8-聯(lián)通”填充效果（其中顏色值是1的點(diǎn)就是指定的邊界）：

圖（3） 邊界填充算法實(shí)現(xiàn)

以上就是本文的全部?jī)?nèi)容，希望本文的內(nèi)容對(duì)大家的學(xué)習(xí)或者工作具有一定的參考學(xué)習(xí)價(jià)值，如果有疑問(wèn)大家可以留言交流，謝謝大家對(duì)服務(wù)器之家的支持。

原文鏈接：https://blog.csdn.net/orbit/article/details/7323090