漢諾塔簡介:
我們想要實現的是 讓 a柱上的盤子,移動到c柱上
1層漢諾塔
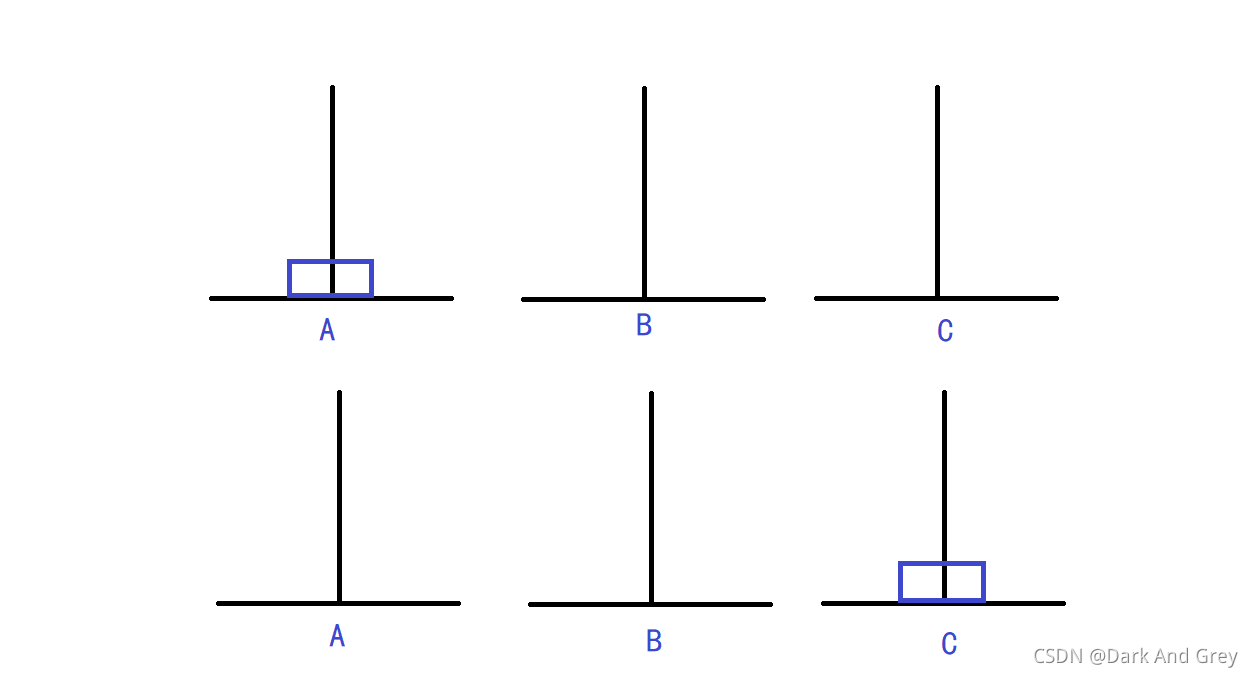
2層漢諾塔
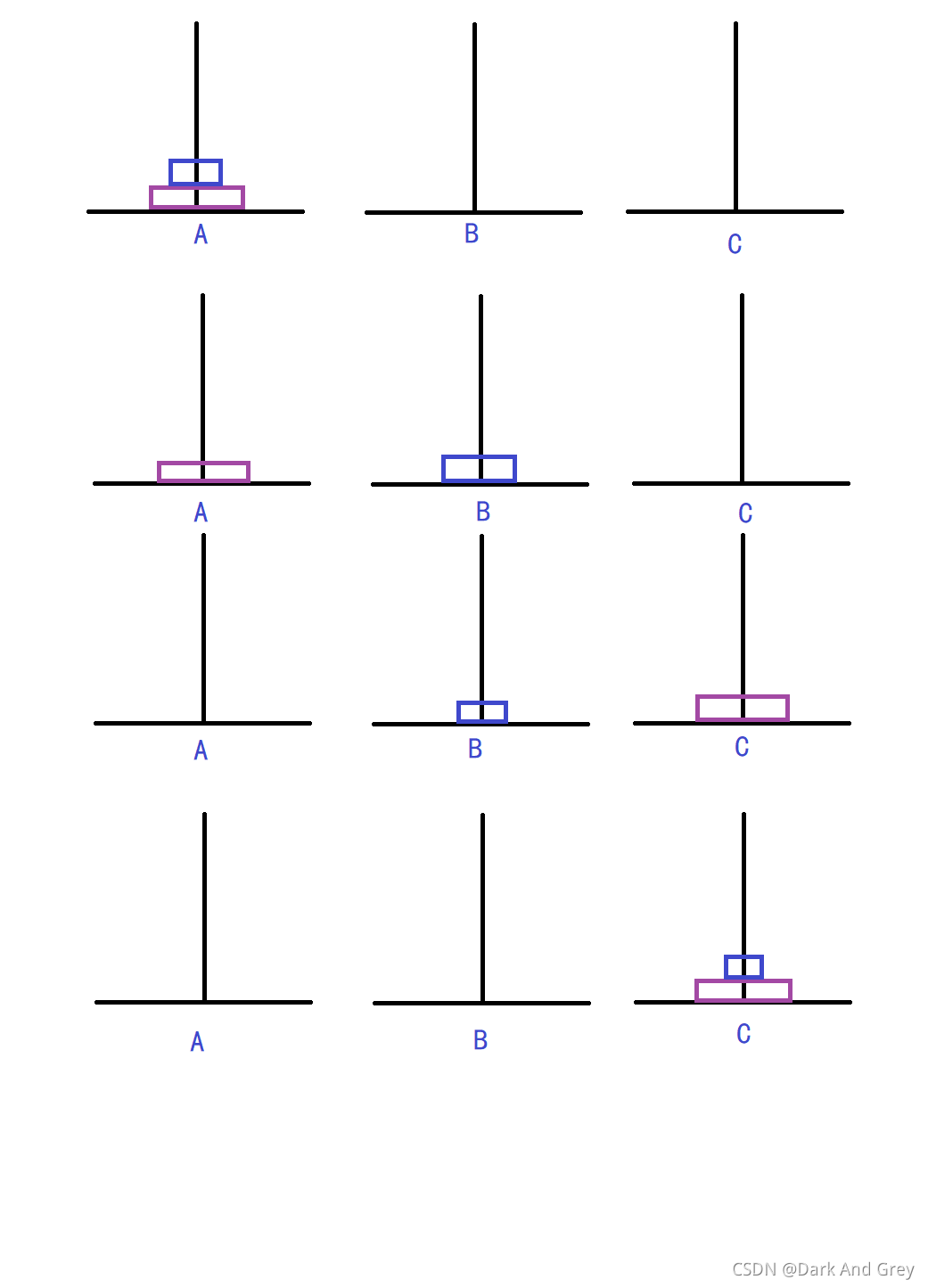
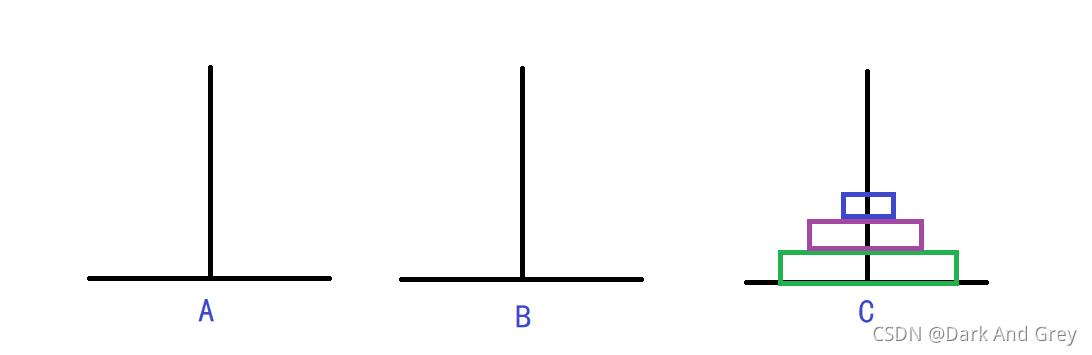
3層漢諾塔詳解圖
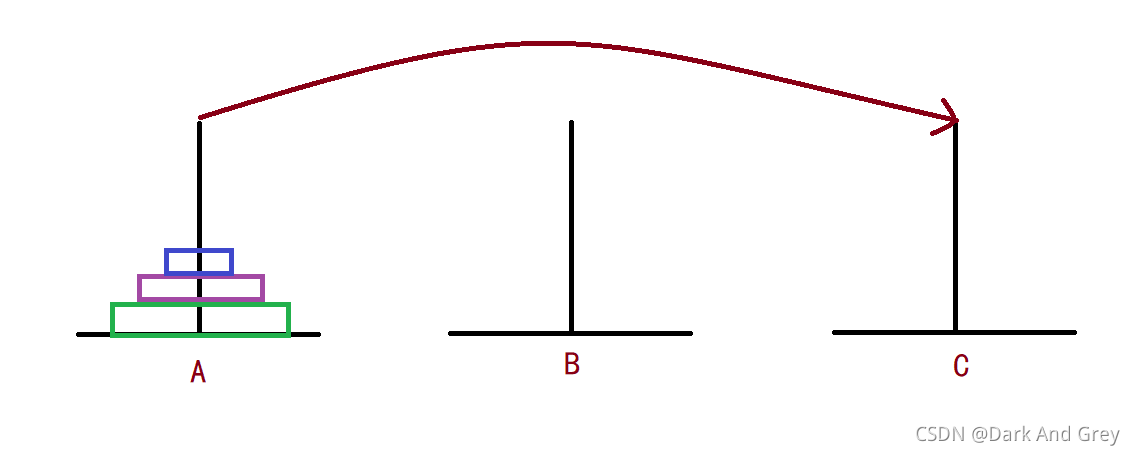
第一步

第二步
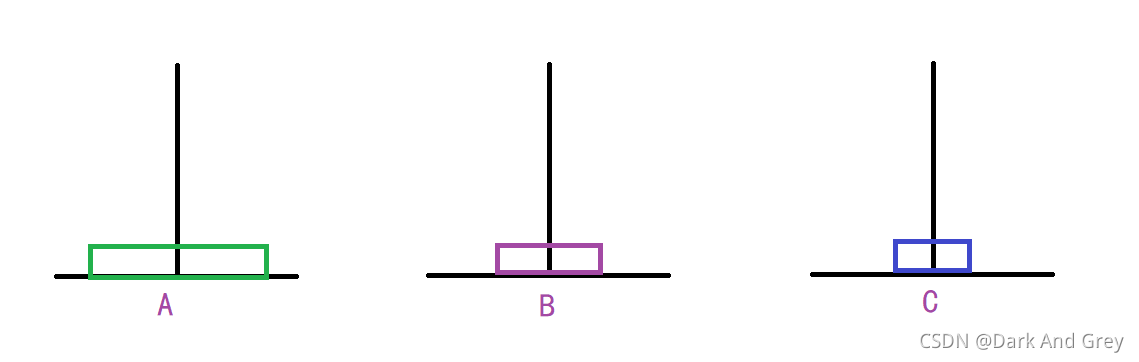
第三步

第四步

第五步
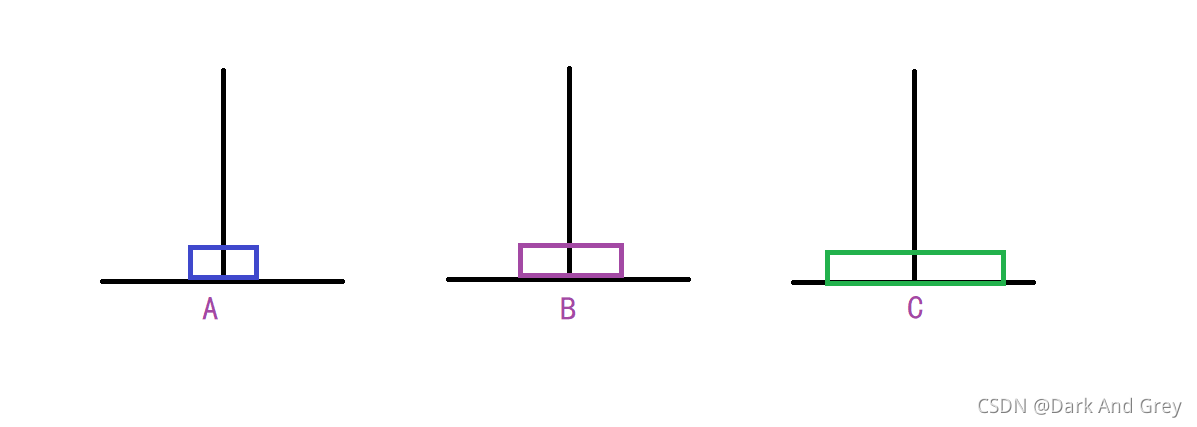
第六步
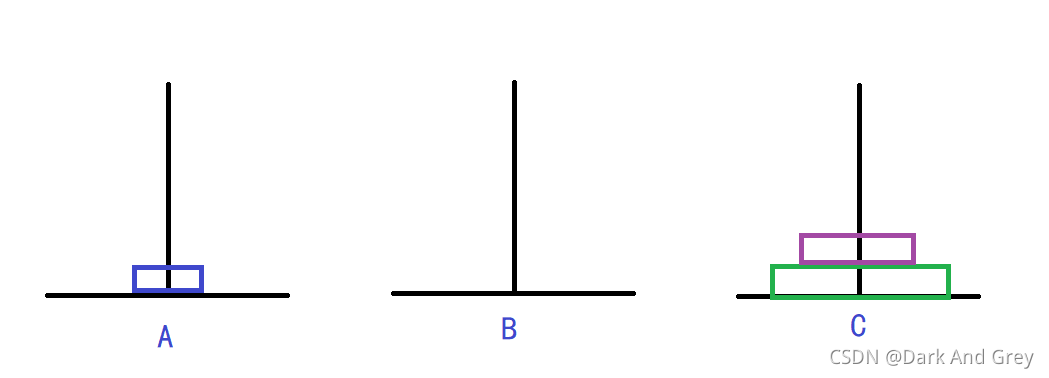
第七步
經過上面的圖解,相比大家一定在一定程度了解到漢諾塔的游戲規則,以及怎么去玩。
總之 最終c柱上第一個盤子,是最大,最頂的是最小的,而且在操作過程中,前幾步就是為了讓三個柱子中最大的盤子移動到c柱上,
然后不斷,將它兩個柱子中最大盤子往上累加,(盤子從大到小,從下往上擺放)
而且盤子一多,你就會發現過程中間,除了最大的盤子,其余的盤子都會集中在 b柱上,這樣才能把 a 柱上最底下也是最大的盤子,移動到c上。
這是規律一
還有一個規律,在最大的盤子移動c柱上之后,第二個大的盤子要放在a柱上,其余盤子按照規則全部放在b柱上,
這樣第二大的盤子才能移動到最大的盤子上
說白了,盤子再多,也要按照上面兩個規律,才能完成整個游戲
那我把最大盤子上面的所有盤子看成一個整體,放在b柱上,最大盤子移動到c柱上,把b柱上盤子直接蓋上去,不就行了,反正也就是重復那兩個規律而已

程序如下
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
import java.util.scanner;public class manuscript { static int times;// 移動次數 public static void main(string[] args) { scanner scanner = new scanner(system.in); char a = 'a'; char b = 'b'; char c = 'c'; int n = scanner.nextint(); game(n,a,b,c); scanner.close(); } public static void move(int disk,char m,char n){ system.out.println("第"+(++times)+"次移動,盤子"+disk+" "+m +"---->"+n); } public static void game(int n,char a,char b,char c){ if(n==1){ move(n,a,c);// 把a柱目前最大盤子放在c柱上,第一次肯定最大的那個 }else{ // 將 n-1 個 盤子 放到b柱子,注意abc位置,再看看下面 move(n,a,c);,細細琢磨 game(n-1,a,c,b);// a b(c) c(b) move(n,a,c); // 把n-1 個盤子 放在c上,注意acb位置 game(n-1,b,a,c);// a(b) b(a) c } }} |
3層漢諾塔的輸出結果附圖(可以返回去看看,對一對)

有什么疑問,可以在下方討論,切記 不要自己帶入一個特別大數字去展開,帶入一個 1 ~3 ,了解規律就行。不主張展開,主張掌握規律(遞推公式)。
本文結束。
以上就是java 實現一個漢諾塔實戰練習的詳細內容,更多關于java 漢諾塔的資料請關注服務器之家其它相關文章!
原文鏈接:https://blog.csdn.net/DarkAndGrey/article/details/120924413